기초 데이터 분석 방법 - 확률부터 가설검정, 베이지안 추론까지

돌아서면 까먹는다

2019-02-27

가설검정, 데이터 분석, 베이즈 확률론, 베이지안 추론, 확률과 통계

문제의 시작

회사에서 검색어를 기반으로 유저의 니즈를 추정하는 업무를 맡게 되었다.
예를 들어 강남 맛집 이라는 검색어에 대한 유저의 니즈는 강남역 근처의 맛있는 음식점 이다.

이번에 유저의 니즈를 파악해야 할 검색어는 스키복할인매장 이다.
검색어 스키복할인매장 을 입력한 유저들이 찾는 장소가 다음중 어느것 일까?

스키타러 가다보면 보이는 외곽지역에 있는 창고형 할인 매장 같은 느낌의 장소인지?
아니면 스키복을 파는 모든 장소인지? (어짜피 다 할인중이니까!!)

위 문제를 얼렁뚱땅 내 느낌으로 말고 데이터에 의거해 판단해 보기로 했다.

스키복할인매장 을 검색한 유저의 로그를 분석해서 (1) 또는 (2) 로 분류 한다
그리고 통계적 추론?을 통해 최종 결론을 내린다.

일단 1번 스텝에서 로그를 분석해서 분류 하는 부분은 하나씩 로그를 열어봐서 유저의 패턴을 찾아야 되는 상황이다.
그러면 가지고 있는 로그 중에 몇 개를 샘플링 해서 수동으로 해야겠다.
그리고 그 결과를 바탕으로 통계적 추론 도구를 적용해 보면 되겠다는 생각이 들었다.

이렇게 생각하고 통계적 추론 도구로 덜컥 베이지안 추론 을 집어 들었다.
베이지안 추론을 집어 들은 이유는 아래 링크에서 데이터 사이언티스트가 갖추어야 할 스킬로서 Bayesian inference 라는 단어를 보았기 때문이다.
https://brunch.co.kr/@hero4earth/3
(그렇게 하면 안되는 것이었다..)

그렇게 무식한 나는 베이지안 추론 -> 베이즈 정리 -> 베이즈 이론? -> 베이즈 확률 -> 확률 -> 통계 -> 가설 검정 … 의 늪에 빠져든다. (이해가 안되니 다른걸 참조 참조 참조.. ㅠㅠ)

나의 무식함을 탓하며 깊은 늪에 빠졌다가 빠져나오면서 순서대로 정리 해본다.
늪에서 발견한 이 모든것의 시작점은 확률 이다.

확률

중고등학교때 배운 확률과 통계 과목을 떠올려 보자.
(안 떠오른다. 그냥 상식적으로 생각한다.)

보통 이렇게 확률이라는 단어를 사용했다.

동전 하나를 던졌을때 앞면이 나올 확률은 1/2 이다.

근데 실제로 동전을 던져보자

동전 하나를 실제로 100번 던졌는데 앞면이 52번 나왔다.

당연한 말인데, 이걸 정확히 뭐라 부르는지를 못해서 베이지안 추론 에서 여기까지 굴러왔다.
같은 내용을 관점에 따라 다르게 표현한 것이다.

엄밀히 말해 동전의 앞면이 나올 확률이 1/2 이라고 할때는 몇가지 가정이 포함된다.

동전의 가장자리의 면적은 0이다
동전의 앞, 뒷면의 면적이 같다
동전을 던질때 공기의 흐름 등 어쩌구 외부적인 요인은 없다.

이를 바탕으로 확률을 계산하면 ‘이상적인’ 확률이 등장한다.
이 1/2 이라는 값을 수학적 확률 이라고 한단다.
이건 계산상, 즉 이론상이고..

현실에 있는 동전을 실제로 던져보면 동전은 분명 앞면 또는 뒷면이 나오고, 동전이 세워지기도 한다…
한 100번 던지면 실제로 앞면이 52번이 나오는 경우도 있고, 43번 나올수도 있는거다
그러면, 100번 던져서 52번 앞면이 나왔으니까 이렇게 말해도 될까?

이 동전을 던져서 앞면이 나올 확률은 52/100 이야

아 여기부터 좀 애매해진다. 상식적으로는 이렇게 말할 수 있다.

(학교에서 배웠다는 말투로) 야.. 그 동전을 무한히 던지다 보면 확률은 1/2 이 될꺼야..

이처럼 현실에서 확률은 어떠한 확정된 결과로 나타나고, 이를 모아서 일련의 데이터로 취급한다.
또는 반대로, 현실에 있는 다양한 데이터를 수집해서 사건의 확률을 계산 해 내기도 한다.

그런데, 이렇게 계산한 확률을 가지고, 아직 일어나지 않은 일이 어떻게 될것인지 예측해 보는것도 가능하다.
예를 들어, 어떤 이상한 동전이 있는데, 아무리 봐도 이건 1/2 로 앞면이 나오지 않을꺼 같이 생긴거다.
(휜거 같기도 하고 뭐 그런느낌)
그래서 이걸 100번 던져봤더니 앞면이 46번 나왔다.
그래서 이런 결론을 내려 봤다.

이 동전을 던져서 앞면이 나올 확률은 1/2 보다 작다.

자, 이 주장을 믿을 수 있을까?
100번 던져서 앞면이 46번 나왔다니까 1/2 보다 적은건 맞는데,
그렇다고 이 테스트 결과에 의거해 이 동전을 가지고 하는 도박에서 뒷면에 돈을 더 많이 베팅 할 수 있겠느냐 이거다.

좀 불안해서 100 번을 더 던져서 앞면이 49번 나왔다.
그러면 이걸 믿을 수 있는건가?
차라리 무한히 던져보면 어떨까? 무한히 던졌더니 48/100 의 확률이 나온다면 전재산을 가지고 뒷면에 계속 베팅하면 결국 돈을 딴다는 거잖니.
근데 당장 돈걸어야되는데 언제까지 무한히 던져야 하는건가..
얼마나 동전을 더 던지면 되는걸까?

이 질문에 답을 찾다보니 통계가 등장했다.
정확히는 Frequentist (빈도주의) 통계의 영역이 등장한거다.

빈도주의 통계와 가설검정

빈도주의 통계?
나에게는 매우 생소한 단어였다. 빈도주의와 구분되는 단어는 베이지안 이다.
뭐 두가지 학파? 가 있다는 것으로 이해 했다…
그리고 보통 접할 수 있는 통계는 빈도주의 통계라고 한다..
(그치만 요새 머신러닝 때문에 베이지안도 많이 들을 수도 있다.)

빈도주의와 베이지안 사고방식의 차이는 아래 블로그에서 잘 설명 해 주셨다.
https://blog.naver.com/bestian/10095013721

위 블로그를 참고해서 우리의 이상한 동전에 대해서 빈도주의적인 접근을 해보자.

(귀무가설) 이 동전도 보통 동전이라면 1/2 확률로 앞면이 나올 것이다.
(대립가설) 근데 내눈에는 이 동전이 휘어 보여서 1/2 확률로 앞면이 나올거 같지가 않다.
그럼 실제로 좀 던져본다. 총 100번 중에 앞면이 46번 나왔다.
그럼 통계 이론에 따라 좀 계산을 해본다. 결과에 따라 동전이 휘었는지 안휘었는지 판단한다.

그럼 ‘4. 통계이론에 따라 계산’은 어떻게 풀면 될까?
기존의 가설 (1. 귀무가설)을 기반으로 확률 분포를 계산하고,
내가 가진 데이터가 이 분포 상에서 있을만한 일이면, 기존의 가설이 맞는것이고,
있을만한 일이 아니라면, 기존의 가설이 틀릴 수 있다는거다.
있을만한 일의 기준은 신뢰수준 이라는 단어를 써서 95%, 99% 등으로 설정하며,
주로 뉴스에서 선거철에 듣는, 이 여론조사는 95%의 신뢰수준이 어쩌고.. 하는 말에서 나오는 그말이다.
95% 신뢰 수준이라는 말은, 100번중에 95번은 가설에 맞는 데이터가 나타난다는 소리란다.
신뢰 수준의 정확한 의미는 여기서 한번 보자
http://mkseo.pe.kr/stats/?p=763

상당히 혼미한데, 이 어려운 내용은 그림으로 보자.

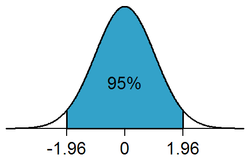
그림 펌 : https://en.wikipedia.org/wiki/Statistical_significance

많이 본듯한 정규 분포 그래프에서 가운데 색칠된 부분이 95% 신뢰 구간이다.
내가 가진 데이터가 95% 의 영역 안에 들어가는지? 아니면 양쪽끝 5% (양쪽이니까 각 2.5%) 구간에 속하는지 보는거다.
그림상 파란부분이 위 설명에 따르면 있을만한 일 의 구간이고, 나머지가 있을만한 일이 아닌 구간이다.

아무튼 됐고, 이제 풀어볼까 하는데, 나는 수학은 1도 모르니까 계산으로는 못푼다. 그냥 그림으로만 보자 ㅎㅎ

동전을 100번 던졌을때 앞면이 몇번 나올지에 대한 그림을 그려본다.
동전 상태는 앞, 뒤 두개밖에 없다고 치면 이항분포를 사용해서 그리면 된단다.
그림 그리기에 쓴 툴 : http://onlinestatbook.com/2/calculators/binomial_dist.html

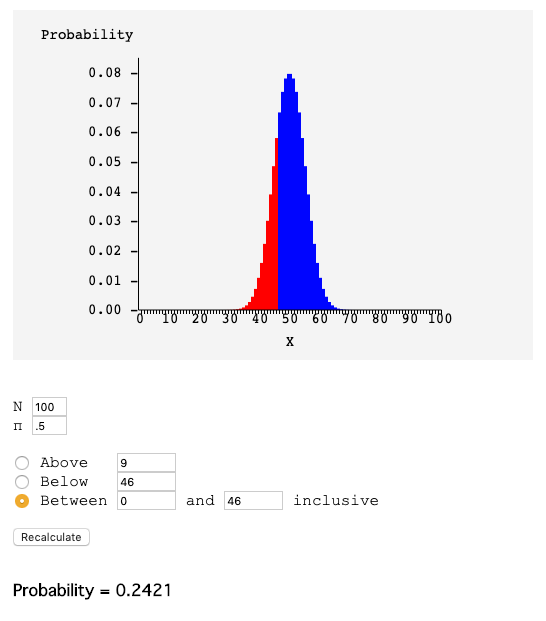
이게 무슨 뜻이냐면, 정상 동전은 100번 던져서 46번 이하로 앞면이 나올 확률이 0.2421 이라는 거다.
그게 무슨 소리냐면 지금 100번 던져서 46번 앞면 나온게 95% 신뢰구간 안에 있는 상황이고, 이건 꽤나 있을법한 일이라는거다.
그래서 대체 이게 무슨 소리냐며는 이 동전은 정상같아 보인다는거다.

아 그럴리가 없어.. 얼마나 앞면이 안나와야 이게 휜것일까?
100번을 더 던졌는데 이번엔 앞면이 39번 나와서, 앞에 케이스랑 합해서 총 200번 중에 85번 정도 앞면이 나왔다고 치고, 그림을 다시 그려본다

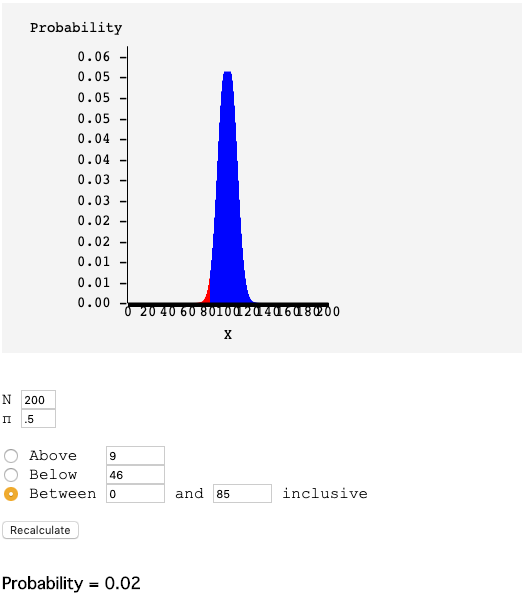
그림대로라면 200번 던져서 앞면이 85번 이하로 나올 확률이 0.02 라는거다.
위의 95% 신뢰구간 그림에서 아랫쪽 2.5% 구간에 우리 데이터가 들어왔다!!
다시말해, 지금 데이터로는 이 동전은 1/2 확률로 앞면이 나온다는 가설로는 잘 안일어나는 일이 일어났고,
그래서 이 동전은 휘었다는 주장을 통계 이론에 의거해 꽤나 신빙성 있게 하게 되었다.

베이즈 확률론

가설검정을 했더니 매우 피곤해졌다.
하지만 여기서 멈출수가 없는데, 간지나는 데이터 사이언티스트가 되기 위해 베이지안 추론을 할줄 알아야 되겠다.
동전던지기를 베이지안 추론으로 어떻게든 해결할 줄 알아야 되는게 아닐까..

베이지안 추론을 검색하고 글을 보다보면 베이지안 xx 라고 자꾸 베이지안 시리즈가 나오는데,
위에서 다룬 빈도주의와 좀 다른 개념으로 확률을 접근한다.
베이즈 확률론 이라고 불리는 이 확률 개념을 보자. (검색하면 베이지안 확률론 이라고도 나온다)
https://ko.wikipedia.org/wiki/%EB%B2%A0%EC%9D%B4%EC%A6%88_%ED%99%95%EB%A5%A0%EB%A1%A0

지식 또는 믿음의 정도를 나타내는 양을 확률로 표현한다는데… 매우 곤란하고 혼란하다.
구지 위의 동전 앞면 1/2 확률에 대해 베이지안 스타일로 말해본다면,

나는 이 동전이 1/2 확률로 앞면이 나올꺼라고 믿는 양이 많아…

정도일려나..ㅜㅜ (그냥 헛소리 같다)

동전가지고 이 소리를 하면 말이 좀 어색하지만, 보통 베이지안을 사용하는 문제의 영역에서는 꽤나 그럴듯한 표현이 된다.

뉴스에서 어떤 병에 걸릴 확률이 1/100 이란다. 조심하래…

위 내용은 빈도주의적 접근을 해서 표본을 구성하고 그중에 몇명이 병에 걸렸는지 세어본 뒤 나온 의미일 수 있다.

100명중에 1 명이 이 병에 걸렸더라. 그니까 병에 걸릴 확률은 1/100 이야. 신뢰수준 95% 에 표본 오차가 어쩌고..

똑똑한 사람들은 가설 검정을 해서 저 확률을 신빙성 있는 주장으로 만들수도 있겠지?
(나는 이제 가설검정 못하겠다..ㅠㅠ)

그럼 좀더 속편하게 베이지안 사고방식으로 말을 해보자 (조금은 덜 배운 베이지안이다)

100명 중에 1명이 이 병에 걸렸더라. 그니까 나는 이 병에 걸릴 확률이 1/100 임에 손모가지를 걸겠어

와 가설 검정을 건너 뛰었다.. 만세!!!
근데 그럼 이런 베이지안 사고방식은 어떻게 신빙성을 갖추는건가? 손모가지로?
가설검정처럼 똑똑해 보이는 복잡한 과정 없이 그냥 나누기 하나로 퉁쳤는데??

사실 답으로 제시한 값은 나누기 한번으로 계산한 것과 같지만, 그 안에는 생략한 말들이 있다.
생략한 말을 포함해서 조금 더 배운 베이지안 사고방식으로 말을 해보자

답이 1/100 이 아니고 다른 값일 확률도 존재 하지만, 현 시점에서 나는 답이 1/100 일 확률이 제일 큰거 같다

베이지안 확률론에서 내가 제일 혼미했던 부분이 확률의 확률을 언급하고 있다는 거였는데,
이거는 어떻게 말로 설명하기 어려우니 좀더 글을 읽다 보다보면 이해가 되길 바란다..
(나도 수많은 예제를 보고 겨우 정리한 말이 확률의 확률이라는 단어다.. ㅠㅠ)

베이지안 추론

아무튼 데이터 사이언티스트 할려면 베이지안 추론을 해야 된다는데. 너무 돌아돌아 왔다.
이제 진짜 베이지안 추론이 뭔지 볼수 있다.
https://ko.wikipedia.org/wiki/%EB%B2%A0%EC%9D%B4%EC%A6%88_%EC%B6%94%EB%A1%A0

추론 대상의 사전 확률과 추가적인 정보를 통해 해당 대상의 사후 확률을 추론하는 방법 이라는데.. ㅠㅠ
수많은 글을 섭렵한뒤, 나는 이렇게 생각하기로 했다.

추론 대상 = 내가 구하고 싶은 사건의 확률
사전 확률 = 기존에 갖고 있는 데이터로 구한 확률 (또는 데이터가 없다면 그냥 그럴듯한걸로 내세운 확률)
추가적인 정보 = 이제 새로 구한 데이터
사후 확률 = 기존 데이터 + 새로 구한 데이터 까지 합해서 구한 확률

또 다른 말로 표현해보면,
베이지안 추론은 현 시점 (현재 내가 가진 데이터 상황)에서의 답을 말하고,
데이터가 추가되면 그 데이터에 맞게 확률을 다시 계산함으로써 결론을 갱신해 나간다.
데이터가 추가될 때마다 결론이 갱신되고, 문제에 어떠한 확률적 경향이 있다면 점점 그 답에 가까워질 것이다.

여기서 데이터 추가, 결론 갱신 이라는 속성이 매우 머신러닝 같지 않은가?
(그래서 베이지안 검색하다보면 머신러닝이 딸려나오나보다)

말이 점점 길어지면서 더 혼미하니까, 예제를 보자.

처음에는 100명중에 1명의 환자를 발견했는데, 추가로 100명을 더 검사했더니 3명의 환자가 더 발견 되었다.

일단그림으로 그려보자.
참고 : https://ratsgo.github.io/statistics/2017/06/30/bayesinfer/
그림 그리기 툴: https://homepage.stat.uiowa.edu/~mbognar/applets/beta.html

위 참고 블로그에 따르면 요건 베타 분포로 그리란다.
처음 조사에서 100 명중에, 1명은 감염, 99 명은 비감염이다.

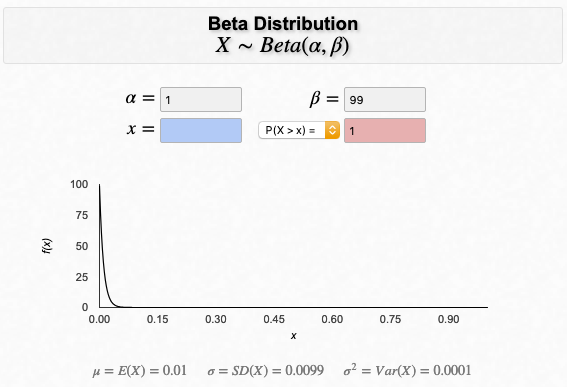
이 그림에 따르면, 그래프가 x 축이 0.01 부분에서 가장 높은데,
이게 감염율이 0.01 일 확률 (y축) 이 제일 크다 (확률의 확률..) 라는 의미란다.
x 축이 0.01 이 아닌 부분에도 확률이 있음을 확인하자.
그치만 그냥 이걸 나같이 덜 배운 사람은 편하게 이렇게 말한다.

이 병에 걸릴 확률은 1% 야..

그러면 추가 검사한 내용까지 포함 해보자.
이제 200명 중에, 4명은 감염, 196명은 비감염이다

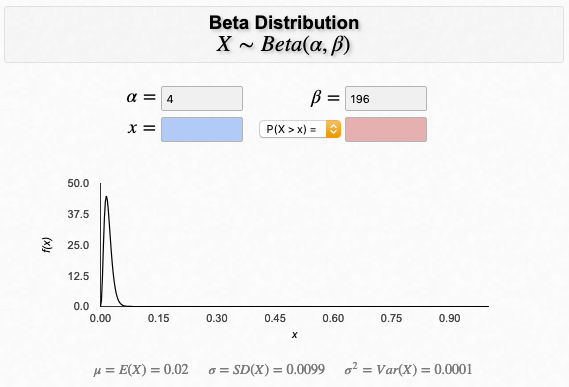
이제 데이터가 업데이트 되고, x축이 0.02 부분이 제일 높다.
이건 이렇게 편하게 말한다.

이 병에 걸릴 확률은 이제 2% 야..

다시 혼미하게 말해 보자.

“이 병에 걸릴 확률은 2%” 라는 확률이 제일 커.. (혼미)

그러나..

열심히 공부해서 말만 혼미하게 했지, 결국 4/200 계산했다..
다음에 더 복잡한 문제가 나왔을때 쓸 일이 있겠지.. ㅠㅠ
(하지만 더 복잡한 문제가 나오면 손도 못댄다고 하더라)

다시 문제로 돌아가서..

‘스키복할인매장’ 검색어를 입력한 사람은 대체 무슨 생각이었을까?
이게 처음의 문제였다.

베이지안 추론의 마지막 단락에 의거하여 내린 결론은,
그냥 로그 분석해서 그중에 몇개가 창고형 할인매장의 니즈를 갖추었는지 세어보고, 나누기 하면 끝이라는거다…
그러면 대략 이런 말을 하게 될것이다.

“스키복할인매장 검색어를 입력한 사람이 창고형 할인 매장을 찾고 있었을 확률이 xx%” 라는 확률이 제일 커.. (혼미)

로그 분석을 자동화 하는데 시간을 쓰는게 낫겠다.. ㅠㅠㅠㅠ
(왠지 여기도 머신러닝 -> 베이지안 xx 의 혼미한 구간이 나타날꺼 같다는…)

그 외 삽질

베이지안 추론과 베이지안 정리는 공식은 비슷하게 생겼지만, 풀고자 하는 문제의 도메인이 많이 다르다
둘을 같이 공부하다보면 매우 혼미해진다

참고

그래프 그리기 참고

그래프 그려주는 사이트 모음
https://easy7.tistory.com/17